
まさしくお宝映像見つけちゃいました!
avexさんありがとう!消さないでネ!
まずは冒頭の20秒をご覧ください!
メッチャ綺麗な螺旋(らせん)

これこそが小説『博士の愛した数式』に出てくる式
\[\Huge e^{i\pi} + 1 = 0 \]
その元になったのがオイラーの公式
\[\huge e^{i\theta} = \cos\theta + i\sin\theta \]
の直感的なイメージです
この螺旋(Choo Choo TRAIN)はガウス平面という所を舞台にします。(OKAXILEはガウス平面で踊ってたんですね〜!)
まずはそれがどんなものか?を見ていきましょう…
ガウス平面
大天才数学者のオイラーくんが70歳の時(1777年)に、天才のバトンを受け継ぐかのように大天才ガウスくんが生まれました。
このガウスくんが考えたのがガウス平面(複素平面)です
200年以上前にこの世に産み落とされ忌み嫌われ続けた\(\huge \; i \;\)に、ガウスくんが真の命を授けたのです!
ガウス平面の作り方
まずはフツウの数直線です

左はマイナスに、右はプラスに、どこまでも続く直線です。\(\LARGE \; \pi \;\)は3.14…なので、だいたい青い↓の所ぐらいですね。そして\(\LARGE \; \frac{\pi}{2} \;\)はその\(\LARGE \; \frac{1}{2} \;\)なので、だいたい緑の↓の所ぐらいです。
で、問題は\(\LARGE \; i \;\)です
\(\; i \;\)は方程式の解を作るために生み出された数字で、2乗すると(-1)となる数字です。数式で書くとこんな感じです
\[\huge i^2 = -1 \]
どんな数(実数)を2乗しても必ず0以上になります。ということは、絶対に\(\LARGE \; i \;\)はこの数直線上に存在しません! で… 天才ガウスくんは何を思ったのか、数直線の原点から上へ線を伸ばして、そこが\(\huge \; i \;\)の場所だ!としました。図で書くとこんな感じです…

これを一旦受け入れると、プラス方向(上方向)には\(\large \; i, 2i, 3i \;\)… マイナス方向(下方向)には \(\large \; -i, -2i, -3i \;\)…と無限に続く数直線が原点から伸ばせます!

これと全く同様に数直線上の任意の点から上下に\(\huge \; i \;\)の軸が伸ばすことができます
これで出来上がったのがガウス平面です

例えば\(\; 2+3i \;\)は赤い丸の点に対応します
数学の言葉でいうと、実数は横軸の数直線上の1点に対応し、複素数(\(\; a+bi \;\))はガウス平面上の1点に対応するのです。
さぁ舞台(ガウス平面)が整いました…
この美しい舞台で複素数が踊りだします
さぁ!Choo Choo TRAIN だ!
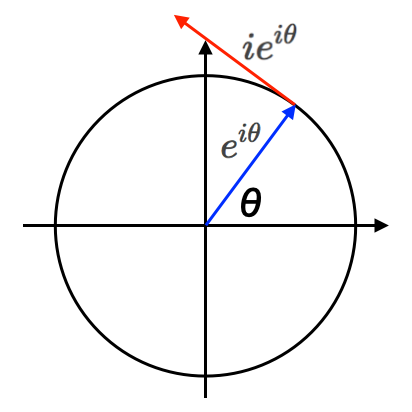
まずガウス平面の中心に半径1の円を書きます
そして円周上の点(図の赤丸)を角度\(\large \; \theta \;\)を使って書いてみると…

そうオイラーの公式の右辺が出てきました
\[\huge \cos\theta + i\sin\theta \]
ガウス平面を重ね合わせて\(\large \; \theta \;\)の軸で串刺しにしてみましょう

すると\(\; \theta \;\)が増加すると赤い点が回転する螺旋が出現しました!
一方、Choo Choo TRAINの画像を見直すと…
まさにリアル オイラーの公式www

元の式がこうなので…
\[\huge \cos\theta + i\sin\theta \]
この螺旋を上からみると

縦軸が実数軸、横軸が\(\large \; \theta \;\)軸になってcosカーブが出てきます

一方、横から見ると

縦軸が\(\LARGE \; i \;\)軸、横軸が\(\large \; \theta \;\)軸になってsinカーブが出てきます

いかがですか? 無味乾燥に見えた式が超リアルなダンスになりました!
オイラーの公式の成立
さて、オイラーの公式の右辺\(\;\cos\theta + i\sin\theta \;\)はガウス平面での円周上の点の動きだということはわかりました
では左辺\(\huge \;e^{i\theta}\;\)は一体何でしょうか?
\(\large \;e\;\)はネイピア数と呼ばれる定数で約2.7です
では\(\large \;e\;\)の\(\; i\theta \;\)乗って何なんでしょう?
普通の感覚では想像がつきませんね…
でも天才オイラーくんはこれに数学的な意味を授けました。しかも全てがつながるように自然で美しい意味を!
とりあえず微分!
オイラーの公式を導く方針としては、右辺の式の構造をしっかり調べて、それが左辺と同じになる、という風に持って行こうと思います。
じゃ、とりあえず乾杯は微分で!www
ということで… \( \; f(\theta) = \cos\theta + i\sin\theta \; \)を微分してみましょう
\[\large f'(\theta) = -\sin\theta + i\cos\theta \]
もう一杯!(それを更に微分すると…)
\[\large f''(\theta) = -\cos\theta - i\sin\theta \]
もう一杯!(それを更に微分すると…)
\[\large f'''(\theta) = \sin\theta - i\cos\theta \]
最後の一杯!(それを更に微分すると…)
\[\large f''''(\theta) = \cos\theta + i\sin\theta \]
元に戻った!
図にするとこんな感じ…

4回微分すると元に戻る
2回微分すると符号が反転…
う〜ん… どっかで聞いたことが…
そうか!1回微分すると\(\large \; i \; \)を掛けたことになってる!
ということは… \(\large \; e^{i\theta} \; \)と同じだ!
つまり\(\; \large \cos\theta + i\sin\theta = e^{i\theta} \;\)だ!
テイラー展開からの〜
なんか騙された感じがするでしょ!
それもそのはずです… 数学的な言葉で言うと
左辺 \(\large e^{i\theta}\) も
右辺 \(\large \cos\theta + i\sin\theta \) も
どちらも微分方程式\(\large \frac{d}{dx}f(x) = if(x) \)の解である、という事しか言っていません… では、左辺から右辺をちゃんとコツコツ導いてみましょう!
まず指数関数\(\large \;e^{x}\;\)をテイラー展開します(テイラー展開の簡易的な証明は最後に載せました)
\[f(x) = f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots\]
\[e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots\]
この指数関数のテイラー展開の式は、よ〜く眺めると各項は高々\(\large \; x \; \)の多項式です。
ここで天才オイラーくんは考えました…
これって複素数でも
いけんじゃね?
実際、\(\; x \;\)に\(\; i\theta \;\)を代入してみると
\[e^{i\theta} = 1+\frac{i\theta}{1!}+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}\cdots\]
\[ = 1+i\frac{\theta}{1!}-\frac{\theta^2}{2!}-i\frac{\theta^3}{3!}+\frac{\theta^4}{4!}+\cdots\]
となります
計算が得意だったオイラーくんは…
ん?どっかで見たことある!
あ!ひらめいた!

これって… 結局…
\[\huge e^{i\theta} = \cos\theta + i\sin\theta \]
っていう事!?
ヤバい!めっちゃ美形やん
っていう感じだったんでしょうか…
数学的な言葉で言うと、「指数関数を複素数に拡張してみたら、何と!隠れていた三角関数が浮き出てきた!」ということになります。
微分がキモ
テイラー展開を使った公式の確認をしましたが、実は微分がキモなんですよ… つまりこういうことです
テイラー展開の公式を見て下さい
\[f(x) = f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots\]
係数に微分が出てきますよね
指数関数のテイラー展開
\[e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots\]
この式の\(\; x \;\)に\(\; i\theta \;\)を代入した時、実数の項と\(\large \; i \;\)の項が互い違いに出現する構造は、まさに三角関数cosとsinの微分構造と同じになるんです
図にするとこんな感じ…

ちょっと分かりづらかったかな? テイラー展開の係数とcos/sinの微分構造が結びついている事をなんとなく感じ取って頂ければいいです!
で、このcos/sinの微分構造が最初に説明したこの図に繋がってくる、というわけです…

そして『博士の愛した数式』
オイラーの公式で
\[\huge e^{i\theta} = \cos\theta + i\sin\theta \]
\(\large \; \theta \;\)に\(\large \; \pi \;\)を代入すると図の赤丸の点となり

\[\LARGE e^{i\pi} = -1 \]
が成り立ち、博士の愛した数式
\[\LARGE e^{i\pi} + 1 = 0 \]
が導かれます。
やっと博士の愛した数式に辿り着きました! 今までの説明でわかったと思いますが、\(\large \; \pi \;\)は3でも4でもなく 3.14159…じゃなきゃダメだし、\(\large \; e \;\)は2でも3でもなく 2.71828…じゃないとダメなんです! だって、そうじゃないと、この図が成り立たない=オイラーの公式が成り立たないからネ!

\(\Large e^{i\theta}\)の幾何学的意味
ここまではオイラーの公式\(\; \small e^{i\theta} = \cos\theta + i\sin\theta \;\)を解析的に、つまり、計算で説明してきました。ここではもっと直感的に\(\large \; e^{i\theta} \; \)がChoo Choo TRAIN(=ガウス平面上の円運動)だということを示したいと思います。
まず、\(\large \; e^{i\theta} \; \)を微分すると…
\[\large f(\theta) = e^{i\theta} \Rightarrow f'(\theta) = ie^{i\theta}\]
となり、\(\large \; e^{i\theta} \; \)に\(\large \; i \; \)を掛けたものとなります。
図で示すと、青いベクトルの先の点での速度が赤いベクトルになる、ということです。
(ガウス平面で\(\large \; i \; \)を掛けると90°回転する事の詳しい説明は記事の最後を見て下さい。)
で、もう一回微分すると…
\[\large f''(\theta) = i^2e^{i\theta}\]
\[\large \qquad \quad = -e^{i\theta}\]
となって、今度は緑の加速度ベクトルが出てきました。

物理を習った人ならわかると思いますが、常に中心へ向かって引っ張られながら等速に動く運動は? そう!等速円運動ですよね!
等速円運動は下記のリンクに詳しく解説されているので、ご参照下さい。
結局、オイラーの公式の左辺
\[\huge e^{i\theta} \]
も Choo Choo TRAIN だったんですねwww

そして三角関数の加法定理
オイラーの公式
\[\huge e^{i\theta} = \cos\theta + i\sin\theta \]
これが紛れもない事実となった今
指数関数の掛け算が三角関数の加法定理に化けることを見てみたいと思います。
まず(証明は省きますが)指数関数の掛け算の公式は複素数になっても成り立ちます。
\[\Large e^{i\alpha}e^{i\beta} = e^{i(\alpha + \beta)} \]
オイラーの公式より左辺は
\[ (\cos\alpha + i\sin\alpha)(\cos\beta + i\sin\beta) \]
\[ = (\cos \alpha \cos \beta - \sin \alpha \sin \beta) \]
\[ + i(\sin \alpha \cos \beta + \cos \alpha \sin \beta) \]
一方、右辺は
\[ \cos (\alpha + \beta) + i\sin (\alpha + \beta) \]
よって、以下の三角関数の加法定理が成り立ちます。
\[\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta\]
\[\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\]
いちいち計算する手間は必要ですが、テストで公式を忘れたとしてももう大丈夫!ですね…
特にcosの符号を間違えることはありません!
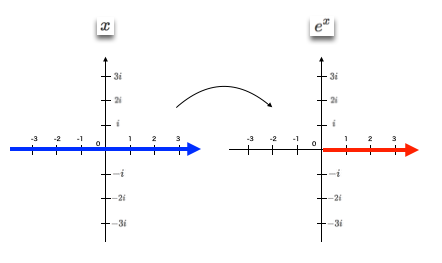
\(e^x\)の形
オイラーの公式に直接関係する内容はここでおしまいです。ここからはもう少しツッコンで関数\(\large \; e^x \;\)の形を見てみたいと思います… なかなか複雑で面白いことが起きますよ!
具体的な説明の前に、まず、関数の定義をちゃんとしておきます。
\[e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots\]
指数関数のテイラー展開の式、この\(\large \; x \;\)が複素数になった関数を考えます。こういう定義域(=変数の範囲)と値域(=関数の値の範囲)が共に複素数となった関数のことを複素関数と呼びます。
なんだか難しそうですね… でも大丈夫!
指数関数の公式\(\; e^\alpha e^\beta = e^{\alpha+\beta} \;\)が使えるので、\(\; x = a + ib \;\)とすると
\[\large e^x = e^{a+ib} = e^a e^{ib}\]
となり、
オイラーの公式より…
\[\large e^x = e^a \cos b + i e^a \sin b\]
となります。
複素数\(\; a + ib \;\)から複素数\(\; e^a \cos b + i e^a \sin b \;\)への写像
ガウス平面の座標でいうと\(\; (a, b) \;\)から\(\; (e^a \cos b, e^a \sin b) \;\)への写像
ということですネ!
では、この関数の形を詳しく見ていきましょう!
まずは普通の指数関数
普通の指数関数は、実数直線の点が正の半直線上の点に写ります。
では、負の半直線に写る元の定義域はどこでしょうか?
そう!\(\large \; a + i\pi \;\)です! 図にするとこんな感じ…

ではでは、\(\large \; i \;\)軸の正の半直線に写る元の定義域はどこでしょうか? そう\(\large \; a + i\frac{\pi}{2} \;\)で、こんな感じ…

そして\(\large \; i \;\)軸の負の半直線に写る定義域は\(\large \; a - i\frac{\pi}{2} \;\)で、こんな感じです

あれ?\(\large \; a + i\frac{3\pi}{2} \;\)じゃないの?
と思った方… するどい!
実は\(\large \; a + i(b \pm 2\pi) \;\)の形の点は全て同じ点に写ります(だって三角関数は周期関数ですもんネ!)
\(\large \; a + i\frac{3\pi}{2} \;\)はグラフの外に出るので、1周期下のを使いました
色々な大きさのChoo Choo TRAIN
オイラーの公式の写像はこんな形になります

じゃ、元の青い線が左によったら?

可愛い Choo Choo TRAIN ができましたね!
元の青い線を右に寄せると…

ダイナミックな Choo Choo TRAIN ができました…
青い線を少し傾けてみると…
じゃ、Choo Choo TRAIN の青い線を少し右へ傾けるとどうなると思います?

答
え
を
見
る
前
に
少
し
考
え
て
み
よ
う
答えはこんな形です(ここから先は定義域と値域のガウス平面を重ねて書きますネ)

どうです? 予想通りでした?
ハートの出現!
なぁ〜んだ!複素関数って簡単じゃ〜ん!と感じてもらえたら、うれしいんですが、どうでしたか? でも元の平面の軌道によっちゃあ、結構複雑な形が出てくるんですよ! ではその様子を見てみましょう!
まず元の平面で Choo Choo TRAIN した場合の軌跡はこんな感じになります。

楕円が少し潰れたおまんじゅうみたいな形になりました…
じゃ、元の平面の Choo Choo TRAIN を少しずつ大きくしていきましょう!
下の図で青円は\(\large \; \frac{\pi}{2}e^{i\theta} \;\)の形をしています

おまんじゅうに明らかな凹みが出てきましたね…
そしてお尻の先は\(\large \; i \;\)軸と接しています(いや〜んwww)
次の青円は\(\large \; \pi e^{i\theta} \;\)の形をしています

するとガチでお尻の割れ目みたいになってきました…
更に元の青円を大きく\(\large \; \frac{3}{2}\pi e^{i\theta} \;\)とします。

するとクロスポイントが出てきました。このようなクロスポイントを特異点と言います。
もっと大きく\(\large \; 2\pi e^{i\theta} \;\)とします。

すると何とハート形が出てきました!
このように重ねて書くと、元の青円は小さくてほとんど見えなくなっていますね!
ここでは赤の曲線の概形だけを示しましたが、実は赤曲線は原点付近でメッチャ複雑な形になってるんです。その形は全体の形と似ていてフラクタル的になるんですが… その辺りの事は、また別記事で書きたいと思います。
[PR]
まとめ
まずはガウス平面という舞台の上で、OKAXILEが踊るChoo Choo TRAINを見ました。
そして、それが指数関数とつながる、まさに、オイラーの公式の成立を確かめました。オイラーの公式を受け入れると、三角関数の加法定理も超カンタンに導けることも見ました。
そして最後に複素関数としての指数関数の形をいろいろ調べました。
さて、オイラーの公式にまつわる色々な話はこれでおしましです。いかがだったでしょうか? 少し難しい部分もあった? 楽しんで数学の自由・美しさを感じることが出来た? もしあなたが少しでもそれを実感できたなら、これに勝る幸せはありません…(おわり)
連載の最初から読みたい方はこちら↓
おまけ
\(\LARGE \; i \;\)を掛けると90°回転する説明
ガウス平面上の点X(\( \; a + ib \;\))に\(\large \; i \;\)を掛けます
すると点Y(\( \; -b + ia \;\))に移動します

図をよくみると緑の直角三角形と黄色の直角三角形は合同なので、点Xと点Yのなす角は90°になります
ベキ級数の収束
テイラー展開
\[f(x) = f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots\]
のような\(\; x \;\)の\(\; n \;\)次式の無限和のことをベキ級数と言います。
本文中では、これが当然収束するものとして扱っていましたが、一般にはベキ級数は収束しないこともあります。ベキ級数が収束するかどうか?を判定する便利な式とかもあるんですが、その説明はこの本をご覧になって下さい。
志賀先生のこの本はメッチャいい本です。複素数・ガウス平面の定義から始まって複素解析の入り口までかゆい所に手が届く丁寧な説明がなされています。
理系の大学1年生の方は是非読んでみて下さい!
テイラー展開の簡易的証明
本文の中で出てきたテイラー展開(マクローリン展開とも言う)の式
\[f(x) = f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots\]
これの簡易的な証明をしてみましょう
関数がベキ級数の形で書けると仮定します。すると
\[f(x) = a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+\cdots\]
という式が成り立ちます。(成り立つような定数列\(\;a_{0}, a_{1}, a_{2}, a_{3}, \cdots \;\)がある。)
ここで\(\; x \;\)に0を代入すると…
\[f(0) = a_{0}\]
テイラー展開の第1項は正しいことが分かりました。
次にベキ級数を1回微分してみます。すると
\[f´(x) = a_{1}+2a_{2}x+3a_{3}x^2+4a_{4}x^3+\cdots\]
が成り立ち、同じく\(\; x \;\)に0を代入すると…
\[f´(0) = a_{1}\]
テイラー展開の第2項は正しいことが分かりました。
これを同じように続けていって、ベキ級数を\(\; n \;\)回微分してみると
\[f^{(n)}(x) = n!a_{n}+(n+1)!a_{n+1}x+\cdots\]
という式が成り立ち、同じく\(\; x \;\)に0を代入すると…
\[f^{(n)}(0) = n!a_{n}\]
結局…
\[a_{n} = \frac{f^{(n)}(0)}{n!}\]
となるのです。
では「関数はベキ級数に書き下せる」という事(仮定)はどこから降ってきたのでしょう? それについてはこのページを読んで下さい。非常に分かりやすく解説されています。
