
ロングテール vs ブロックバスター論争
少し前にマーケティング界隈でロングテール理論が流行りました。これはアマゾンやドンキ・成城石井みたいに超大量の品揃えをして、売上少ないながらもチリツモな商売をするのがイケてまっせ!という理論です。ところが最近
いやいやそれ違うっしょwww
という反対勢力が現れてきました。その名もブロックバスター理論です。
ブロックバスターというのは元々は超強力な爆弾(1区画をふっとばすぐらいすごいヤツ)の事を言うんですが、転じて、劇的に売れる商品、もうそれ1つで売上のほとんどを担うような商品の事をいいます。で、ブロックバスター理論は、そんな商品の開発を全力でやるんじゃ〜〜〜! っていう理論なんです。
実は今、この2つの勢力が拮抗しています。「ロングテール」でググるとわかるんですが、半々ぐらいでそれぞれの陣営のページが出てきます。中には1つの記事の中に「2つ説がある」みたいな書き方をしている物もあります。
では本当の所、どちらが正しいのでしょうか?
結論を先に言うと、ブロックバスター理論が正しいです。しかし、ロングテール理論も完全な誤りとは言い切れない、というのが本当の所です。
それではどうしてそうなるのか?を詳しく見ていくことにしましょう!
21世紀の分布・べき乗分布
まずは論より証拠!百聞は一見にしかず!
実際のデータを見てみましょう!
VALU時価総額ランキング
これはVALU(仮想通貨を使った個人株式市場みたいな物)の時価総額ランキングです。(2017年12月12日)

縦軸を時価総額にし、ランク順に並べたグラフを描くと、こんな感じになります

見事にブロックバスターとロングテールが出てきますね!
べき乗分布・ジップの法則
このままだと分布の形がよくわからないので、X軸とY軸両方とも対数にしてみます。
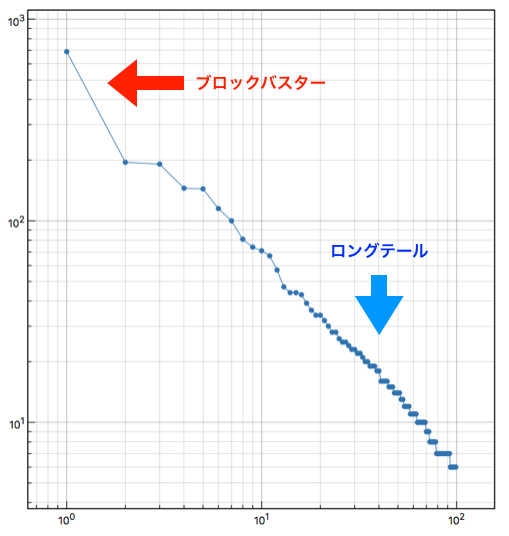
するとどうでしょう!きれいに一直線に乗りました!(2位の人がもうちょっと頑張ってくれたら、もっと綺麗に乗ったのにwww)
このように縦軸に価値、横軸にランク(順位)をプロットして、どちらも対数表示した時に直線となる分布のことをべき乗分布と呼びます。特にその傾きが −1となる時、ジップの法則(Zipfの法則)に従う、と言います。
ジップの法則は極めて単純な法則で
N位の価値は1位の 1/N になる
というものです。実際VALU時価総額の1位は690億円で、10位は71億円、100位は6億円とほぼそのようになっています。
ジップの法則、それは簡単に言うと、一握りのスーパースターと多くの雑魚がいる分布です。富める者はどんどん富み、貧乏人とは別世界に住んでいる… そんな超厳しいお話です。
いやいや現実はもっと貧乏人に優しいっしょ!
と思うかもしれませんが、現実の所得分布の上位1%(日本でいうと上位100万人)はべき乗分布に従うことが知られています。 あぁなんて無情な…
話を元に戻すと… このべき乗分布がキモです。普通の分布、例えば身長や体重の分布にはブロックバスターもロングテールも存在しません。図にするとこんな感じです。

身長が2mの人はいますが、4m、8m、16mという人はいませんよね… しかし、所得は1億円、10億円、100億円の人が出てくるんです…
で、ブロックバスターが生まれるような状況では、このブロックバスターを生み出す努力をすることが得策なのです!
記録はどんどん塗り替えられる
ブロックバスターがハンパない事はわかった。でも、ロングテール、つまり雑魚の大群も重要なんじゃないの!? そうだ!そうだ!貧乏人を見捨てるな〜〜〜!
と、ロングテール理論の声が聞こえそうですよね…
でも残念ながら、どう逆立ちしてもブロックバスターの方が重要なんです…
それはなぜか?というと、この恐竜のヘッドは時間と共にどんどん伸びるからなんです。

つまり、売上記録はどんどん塗り替えられるわけです。
例えば、つい最近もYouTubeの再生回数記録が塗り替えられました。
統計学的な言葉にすると「べき乗分布の上位期待値は、観測時間を伸ばすと無限大に発散する」ということです。(平均値も無限大に発散します)
今となっては既に懐かしいピコ太郎ですが、例えば2020年までにピコ太郎の2倍の再生回数を叩き出すブロックバスター芸人が出現するかもしれません!
そういう想定外の出来事が無視できない確率で発生するのがべき乗分布なのです。
ヘッド?テール?大混乱!
ロングテールという言葉は、今、大混乱しています。というのも、もともとは統計学でロングテール(正確にはヘビーテール)という概念がありました。それは先ほども述べた通り、この図におけるヘッド、つまりブロックバスターの事を指します。

では、なんでヘッドとテールが逆転したのでしょう?それはこういう理屈です。
通常、統計学では横軸に値、縦軸にその発生確率をプロットして確率分布とします。図にするとだいたいこんな感じです。

売上vsランクのグラフのX軸とY軸をひっくり返したのが統計学における確率分布になります。(正確には累積分布なんですが、 べき乗分布の場合その違いは定性的に問題になりません)
そして、その確率分布の値が大きい場所での確率が無視できない。つまり、裾が厚い=テールがヘビーな分布がべき乗分布というわけです。
結局、統計学のロングテール(ヘビーテール)が、マーケティング用語でのブロックバスターになります。
もう何がなんだか、訳がわかりませんよね!
実際、英語のWikipediaでも統計学におけるロングテール(=マーケティングにおけるブロックバスター)と(マーケティングにおける)ロングテールを混同して記述していたりします。
まぁ、言葉の混乱はさておき、実際にどちらが重要か?というと、これまで述べてきたように限界を知らないブロックバスターなのです!
ブロックバスターが誕生する条件
さて、ではどうしたらブロックバスターを産むことができるのでしょうか? それを詳しく見ていきましょう…
SNS(口コミ)が最も重要!
まず、自己増殖的な振る舞い=指数関数的な増加が重要です。悔しいけど、富める者はどんどん富むっていう例のヤツです…
「人気が出れば出るほど、噂がどんどん広まり、もっともっと成長する」という正のスパイラルは、江戸時代はアナログ的な口コミがその媒体となっていました。それが昭和のラジオ・テレビ・雑誌の時代を経て、平成の今はSNSがその媒体となっています。
昔と比べて、ブロックバスターの成長速度は格段に速く、皆んなに忘れ去られるのも格段に速くなりました。今の時代、どんな商品でもブロックバスターになるためにはSNSでバズることが必須です。
生産・流通コストがゼロ
ブロックバスターの成長限界は物理的な制約によって決まります。どうやっても人類は身長4mにはなれないのです!
ブロックバスターをすくすく成長させるためには、成長を抑える原因となる生産・流通コストは限りなくゼロに近づける必要があります。アマゾンの成功も、広告・決済・流通のコストを限りなく抑えることで成り立っているのです。
最初に紹介したVALUがとても良い例です。実際の株式発行だと証券会社やら審査機関やらが絡み、一気にコストがかさんできます。結果として、システムができて1年も経たないうちにあんなに綺麗なべき乗分布が発生するなんて事はありえません。
今、フィーバーしている仮想通貨もそうです。リアルな紙幣を発行する必要がないからこそ急激な成長ができるのです。
ある程度の量が必要
そして、ここがロングテール理論と絡む所なんですが、ブロックバスターが出現するためには、ある程度の量(試行回数だったり、商品数だったり)が必要だということです。
つまり、ブロックバスターがハンパない売上を上げることは間違いないが、その確率はそれほど大きい訳じゃないということです。具体的にいうと、だいたい、1000ぐらいのオーダーの試行なり、商品数が必要です。(ブログでまず100記事書け!理論はまんざら嘘でもないわけです。)
別に売れない商品や読まれない記事を多く作る必要はありませんが、ブロックバスターを生み出すには、それなりな量の経験が必要なのです。(例えばブログだったら、人気のブログを自分ならこう書くぐらいの考察をしながら100記事以上読むことが重要です。)
でも、一発屋芸人みたいにデビューしてすぐにブロックバスターぶちかますケースもあるじゃん!という意見もあると思いますが、それはもちろん確率ですから、そういう事象もありえます。
話を元に戻すと、ブロックバスターを産むためにはある程度な母数が必要、だから、結果的にロングテールが同時に発生するわけです!
人生におけるブロックバスター
人生においては色んなイベントがあります…
「昼飯に食べた立ち食いそば屋が想定外に美味しかった!」とかいう雑魚なイベントもあれば、プロポーズされた瞬間・就職が決まった時・試験に合格した時などの超ビッグイベントもありますよね!(但し、生まれた瞬間と死ぬ瞬間という誰もが必ず通過する一番重要なイベントは除く)
仮に、人生のイベント発生確率が、統計学で言うところのヘビーテールを持っているとすると… いったいどういうことが起こるんでしょうか? それはつまりこういう事になります…
- 1週間に3分(1分 x 3回)ぐらい超重要な事が起こる
- 1年に3時間(1時間 x 3回)ぐらい超重要な時間帯がある
- 10年に3日(1日 x 3回)ぐらい超重要な日がある
- 人生(70年)に3週(1週 x 3回)ぐらい人生を変えた週がある
どうですか? 実際の感覚とあっていますか?
人生の中の多くの時間、多くの日、多くの週は、同じ事の繰り返しに過ぎない極めて平凡な物である。でも、時々、とてつもなく重要な事が起きて、それ(=人生におけるブロックバスター)が人生を方向付ける。
もしこの仮説が正しいならば、人生は正規分布では語れないフラクタルなんですね…
まとめ
まず最初に、ロングテール vs ブロックバスター どちらが本当に重要か?をVALUのデータを見ながら探っていきました。そして、限界を知らないブロックバスター、その背後にあるべき乗分布がキモだということを説明しました。
次に、ブロックバスターが生まれる条件を考え、その要件の結果としてロングテールが発生することを説明しました。
そして最後に人生におけるブロックバスター理論・べき乗分布理論に話を発展させました。
いかがだったでしょうか?納得できましたか?
え?皆んな中流だった昭和が懐かしい?
いや、時代は平成、そして次の年号になるんです! 頭を切り替えてブロックバスター目指して頑張りましょう!
おまけ
ここでは、本編の中ではツッコンで解説できなかった理系的な事を詳しく解説します。分量が多くなってしまいますが、より深くロングテールについて理解できると思います。
ヘビーテール(裾が重い)分布
もう暫くお待ち下さい。
コーシー分布からの〜ジップの法則
もう暫くお待ち下さい。
べき乗則・安定分布・フラクタル
もう暫くお待ち下さい。
この辺りの詳しい解説については、高安先生の名著↓を是非ご覧ください。
